Orientierung von Punkten

2. Punktkonfigurationen zeichnen

Sind eine Reihe von Orientierungen von Punkttripeln gegeben, kann man die zugehörige Konfiguration der Punkte zeichnen. Wie das funktioniert soll am Beispiel der folgenden Orientierungen gezeigt werden:

1. [a,b,c] > 0
2. [a,c,d] = 0
3. [a,b,d] > 0
4. [b,c,d] > 0

Die Orientierungen können in beliebiger Reihenfolge abgearbeitet werden, wir gehen hier von oben nach unten vor.

Zunächst werden a und b eingezeichnet. Da die 1. Orientierung [a,b,c] > 0 ist, muss c links einer gedachten Gerade durch a und b liegen, sodass die Drehung entgegen dem Uhrzeigersinn erfolgt.

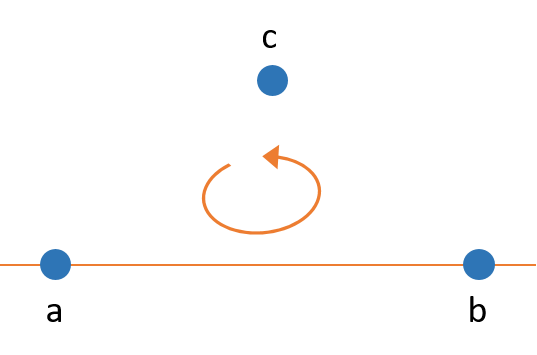
Die 2. Orientierung [a,c,d] sagt aus, dass die drei Punkte auf einer Gerade, also kollinear, liegen müssen. d könnte beispielsweise oberhalb von c liegen.

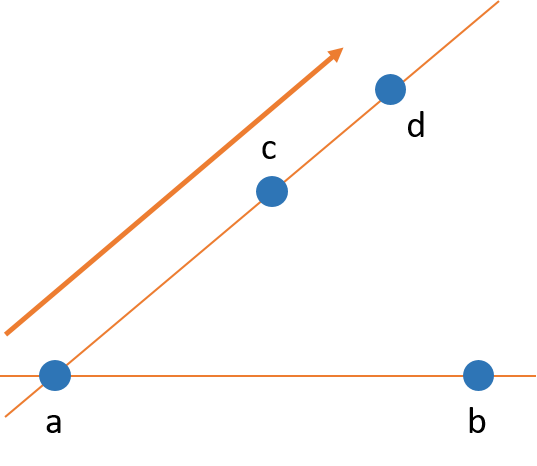
Der 3. Orientierung [a,b,d] > 0 zufolge, muss auch d links der Gerade durch a und b liegen. Das ist bereits der Fall.

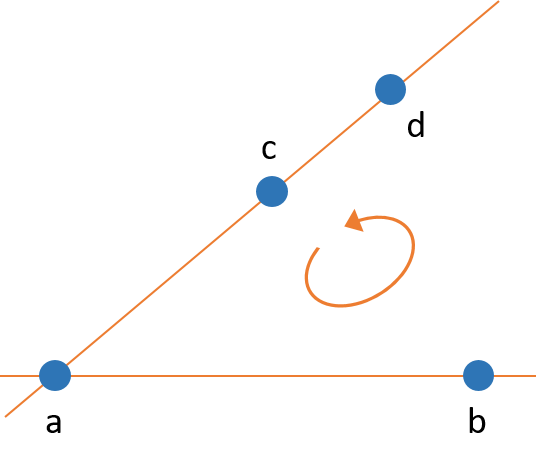
Bei der 4. Orientierung [b,c,d] > 0 gibt es nun jedoch ein Problem. Eigentlich müsste die Drehung von b über c nach d im Gegenuhrzeigersinn erfolgen, ist aber tatsächlich im Uhrzeigersinn. Eine Möglichkeit das zu beheben ist, d zu verschieben. Laut der 2. Orientierung kann überall auf der von a und c aufgespannten Gerade liegen. Die 3. Orientierung schränkt ein, dass d nicht unterhalb von a liegen darf, da ansonsten die 3. Orientierung [a,b,d] < 0 wäre. d muss also zwischen a und c liegen.

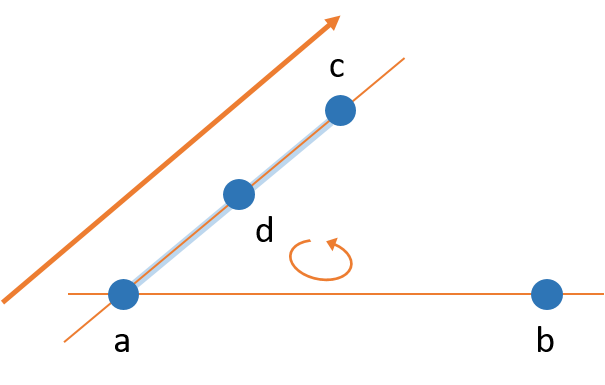
Immer wenn ein Punkt bei der Erstellung einer Punktkonfiguration verschoben wird, müssen nochmals alle Orientierungen, in denen der Punkt enthalten ist, überprüft werden. In diesem Fall wären das die Orientierungen 2, 3 und 4, die aber schon bei der Verschiebung von d in Betracht gezogen wurden.

Da nun alle Orientierungen abgearbeitet sind, ist die vorliegende Punktkonfiguration eine gültige Lösung für die gegebenen Orientierungen.